高考立体几何题100道及答案_高考立体几何题

1.高三立体几何圆锥题求解

2.高三数学立体几何题！

3.立体几何高考题

4.一道立体几何题目 在线等！高三的！

5.具体如何应用矩阵来解决高三的立体几何图形问题？

6.一道高三数学立体几何的题（不要用建系方法做）

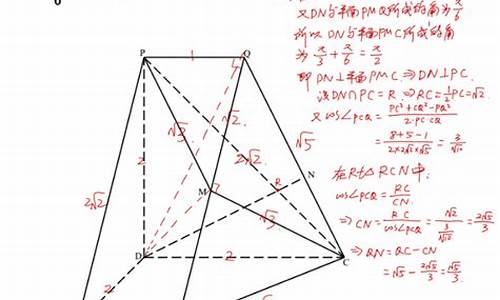
〈BAD=90°，根据勾股定理，BD^2=AB^2+AD^2,BD=√5，

四边形ABCD是矩形，AC=BD=√5，

在平面ABB’A’上作A’M⊥AB，A’N⊥AD,垂足为M，N，

作A’H⊥平面ABCD，垂足H，连结HM，HN，

根据三垂线定理，HM⊥AB，HN⊥AD，

<A’AM=<A’AD=60度，

H点在〈DAB的平分线上，

AM=AA'cos60°=3/2，

△AHM是等腰RT△，

AH=√2AM=3√2/2，

A'H=√(AA'^2-AH^2)=3√2/2,

以A为原点建立空间坐标系，

A（0，0，0），B（1，0，0），C（1，2，0），D（0，2，0），

A'(3/2,3/2,3√2/2),c'(5/2,7/2,3√2/2),

向量AB=（1，0，0），

向量BC=（0，2，0），

向量CC‘=（3/2，3/2，3√2/2),

向量AC’=向量AB+向量BC+向量CC‘

=（5/2，7/2，3√2/2）

|AC’|=√（25/4+49/4+18/4）=√23。

高三立体几何圆锥题求解

对于此类题，建系必须选择合适的原点，若题目未给出合适的原点，可通过所给条件寻找一个合适的点，此题：

∵PA⊥底面ABCD，ABCD为菱形，∴AC⊥BD，设交于O

建立以O为原点，以AC方向为X轴，以BD方向为Y轴，以AP方向为Z轴正方向的空间直角坐标系O-xyz

∵AC=2√2，PA=2，E是PC上一点PE=2CE

则点坐标：

O(0,0,0)，A(-√2,0,0)，C(√2,0,0)，P(-√2,0,2)，E(√2/3,0,2/3)，B(0,-y,0)，D(0,y,0)

向量PC=(2√2,0,-2)，向量EB=(-√2/3,-y,-2/3)，向量ED=(-√2/3,y,-2/3)

向量PC*向量EB =-4/3+0+4/3=0

向量PC*向量ED =-4/3+0+4/3=0

∴PC⊥面BED

(2)∵二面角A-PB-C为90°，∴底面ABCD就变成正方形（也是菱形）就可以如答案建系

高三数学立体几何题！

圆锥高为h=1/2，底面半径为r=√3 /2

设某切面底边与底面圆心距离为a，则：

切面（三角形）的底边长为2√(r^2-a^2)

切面的高为：√(h^2+a^2)

切面面积=√(3/4-a^2) x √(1/4+a^2) = √（1/4-(a^2+1/4)^2）

显然，当a=0时取最大值，面积为√3 /4

立体几何高考题

八个半径为1的球放进去之后，正好放在正方体内，上下两层，一层四个，也就可以看做将棱长为4的正方体切三刀，切成八个棱长为2的小正方体，每个正方体内放一个半径为1的球。最后一个球的球心必定是大正方体的体心，也就是切出的八个小正方体的共同的那个顶点，最后一个球的半径就是这个顶点到半径为1的球的垂线。也就是说，小正方体的体对角线减去小球的直径再除以2就是所求小球的半径。。。。。。。。自己画画图吧，说不太好。。。。。。。

切成8个小正方体的体对角线长：d=根号下（2的平方加上2倍根号2的平方）=2倍根号3

故所求小球半径：r=（d-1X2）/2=根号3减1

一道立体几何题目 在线等！高三的！

1)由余弦定理求得DB=√6*AD=√6*AB/2

PB=√（PD）∧2+（DB）∧2=

PA=√（PD）∧2+（AD）∧2=

用勾股定理，证明三角形PAB是直角三角形即可，即只要PA∧2+AB∧2=PB∧2即可

2)设D点在三角形BPC的垂足为F点，用第一问的方法求出三角形PFD是直角三角形即可求出

具体如何应用矩阵来解决高三的立体几何图形问题？

1,由正方形

CB垂直AB PA垂直平面·ABCD

PA垂直CB PA交BA于A

CB垂直面PAB 所以面PCB垂直PAB

所以二面角C-PB-A为90°

2,过B做BE垂直PC于E 连接DE BD

易得 DE垂直PC

BC=a BP=根2a PC=根3a

BE=根6/3*a=DE BD=根2a

余弦定理得 cos角DEB=（2/3a^2+2/3a^2-2a^2)/(2*2/3a^2)=-1/2

所以角DEB=-120°

即为B-PC-D

不懂再问

一道高三数学立体几何的题（不要用建系方法做）

答:为了使复杂的问题简单化，也便于看图和理解，特作了x0y平面和交线在x轴上的平面来说明问题，至于平面位于何处，两平面交线的位置在哪里，原理都是一样的。详见下图。

从题面的问题来看，有点概念的问题需要澄清，欧几里得立体几何的问题，用不到矩阵，只有向量差积的时候才用到行列式，线性方程的问题才用到矩阵。它不同于非欧几里得几何学。这个题面的问题很大，因为，每一个问题都可以根据出题的不同情况采用不同的方法求得，都进行说明的话，可以写一本书。因此，我只用一种方法说民情况，其余的方法你可以根据原理，举一反三。

1、求二面角平面a和β所成的角：在讲这个问题之前，先要明确几个问题，二面角永远指的都是不大于90度的角；同理，直线与平面的夹角也是不大于90度的角。因此，二面角的三角函数值都是正数，没有负数。直线与平面的夹角的三角函数值也是如此。

根据上述所说的道理，二面角就等于两个平面的法向量的夹角。分别在a和β平面选择两条不相交的直线作为平面向量，a平面可以选取OA和OD，如果不知道A，D两点的坐标，你可以设单位向量OA^0={1,0,0}, OD^0={0,1,0}, 因为你所求的a平面平面法向量是垂直这个平面的方向，所求的只是方向，与数值大小无关。所以你设这两个平面向量的长度多少都可以，只与两个向量的差积方向有关与矢径长度无关。β平面选择OA，OB，B点坐标为：(Bx,By,Bz),na=OA^0xOD^0={1,0,0}x{0,1,0}={0,0,1}; 在这里要用到行列式,具体算法如下：

cos(a,^β)=nβ·na/(|nβ|*|na|)={0,Bz,By}·{}0,0,1}/(|nβ|*|na|)

=(0*0+Bz*0+By*1)/[√(0^+Bz^2+By)^2*√(0+0+1^2)]=By/√(Bz^2+By^2)。

二面角(a,^β)=arccos[By/√(Bz^2+By^2)]。

总结求二面角的过程，我们运用了行列式、差积、点积（包含了混合积）、两点间的距离（线段的求法）、法向量的求法、余弦值和角度的求法。

2、通过求直线AB与平面β的夹角，再强调一下线段的求法，线段的求法，就是把线段看作是向量，求矢径，也是求两点间的距离。A的坐标(Ax,Ay,Az)=(Ax,0,0), B-(Bx,By,Bz), 向量AB={Bx-Ax,By-Ay,Bz-Az}={Bx-Ax, By,Bz}, 矢径|AB|=√[(Bx-Ax)^2+(By-Ay)^2+(Bz-Az)^2]；既是AB线段的长度，也是A、B两点间的距离。现在设AB与平面β夹角为γ：作OC//=AB，那么，OC=AB； OC与平面β的夹角γ，就是AB与平面β的夹角γ,而AC（AB）与法平面nβ的夹角为（90D-γ）；sinγ=cos(90D-γ)=AC·nβ(|nβ|*|AC|)=[(Bx-Ax)*0+By*0+Bz*1]/{√[(Bx-Ax)^2+By^2+Bz^2]*√1}=Bz/√[(Bx-Ax)^2+By^2+Bz^2]。

3、因为所有的平面角和二面角都在区间[0,90D]的范围内。已知余弦值，可以利用三角函数公式来求其它三角函数：sinθ=√[1-(cosθ)^2], tanθ=sinθ/√[1-(cosθ)^2], cotθ=1/tanθ.

到此，题面的问题全部答完。但是，这只是基本的方法，要解决实际问题，必须多做题才能真正掌握做题的技巧，才可以把题做的简单而清晰。才能够体现出把复杂的问题简单化的数学思想，才可以领悟数学之美。

作DF⊥BC于F,易知DF⊥平面BCC'B',A'C'⊥平面BCC'B',

连C'F,D是AB的中点，∠ACB=90°，

∴DF∥AC,F是BC的中点，

又E是BB'的中点，AC=BC=AA′，

∴C'F⊥CE,

∴A'D⊥CE.

(2)作正方体ACBG-A'C'B'G',设H是GG'的中点，易知

AH∥CE,

∴∠C'AH是AC'与CE所成的角。

解△AC'H,就可得cos∠C'AH.

余下部分，留给您练习，可以吗？